corCTF 2025 - whatever-floats-your-boat
- Author: maxster
- Date:
corCTF 2025 - whatever-floats-your-boat
Well… how the heck did I end up here?
whatever-floats-your-boat was my favorite challenge that I made for corCTF 2025.
I had an absolute blast writing this challenge and learning about the mechanics of floating point arithmetic.
The rev challenge used a virtual machine based around several absolutely cursed concepts: IEEE 754 floating-point arithmetic and the x86 MXCSR FPU exception flags. In this blog, I will talk about the VM design and how floating-point algorithms were put together in order to create the challenge’s flag calculator program.
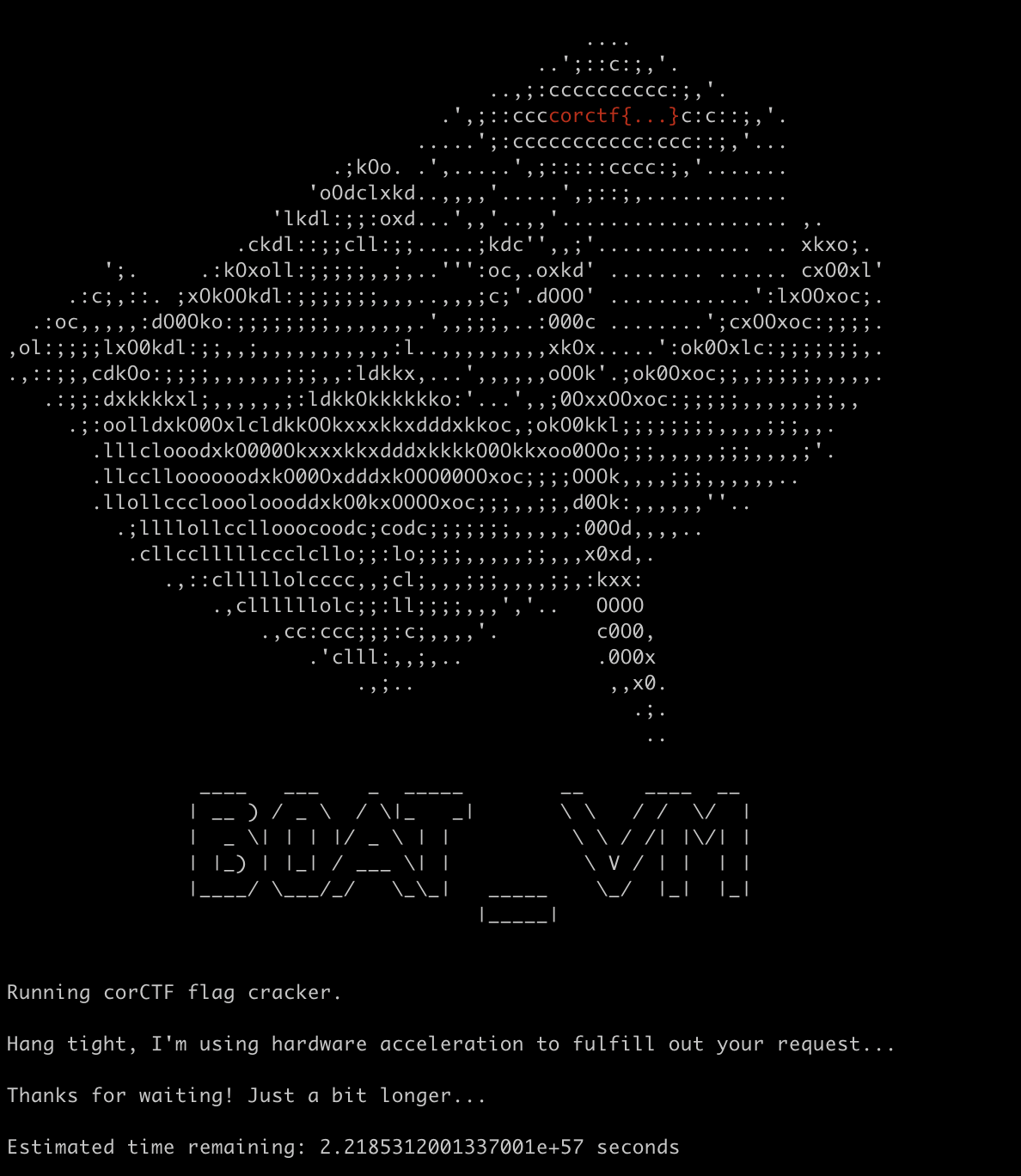
The CTF challenge provided a VM binary as well as a 60-kilobyte program which promised to print the flag. Just one problem… this program isn’t expected to finish anytime within the next 10^50 years. By then, most of the matter in the universe will have condensed into supermassive black holes or clouds of gas.
Clearly, there must be a more efficient way to solve this challenge. In order to obtain the flag, players must understand what the VM is doing.
The Virtual Machine

The idea for this VM originally came from my friend Timothy Herchen, but he didn’t have the time to turn this amazing concept into a challenge for corCTF. As “head of rev dev,” I decided to take it into my own hands and implement the idea into a rev challenge. Thanks, Timothy!
As mentioned above, this VM is based entirely around the behavior of IEEE 754 floating-point arithmetic. x86’s SIMD extensions offer the
LDMXCSR and STMXCSR instructions to access the MXCSR (Media eXtension Control and Status Register) state
for programs to get and reset the exception flags raised by floating-point calculations.
The way boat-vm actually works is fairly standard, and is modeled after WebAssembly and the Java Virtual Machine.
The VM contains a data stack and a separate function call stack, and the destinations of CALL/RET instructions
are statically encoded into the instruction — there is no arbitrary “jump to the address in this register.” Outside of the data stack, there exist LOAD and STORE opcodes, which allow for random memory access.
However, the way the VM handles branching logic is very peculiar. Instead of usual “branch if zero” or
“branch if nonzero” opcodes, branching behavior is decided using the
B_DIVBYZERO, B_INEXACT, B_INVALID, B_OVERFLOW, B_UNDERFLOW,
instructions, which read the FPU’s exception state to determine whether to take a branch.
In order to use this primitive, there was also a CLEAR_EXCEPT instruction which would
reset the MXCSR register for future use. In C, this was implemented using immintrin.h’s _MM_GET_EXCEPTION_STATE() and _MM_SET_EXCEPTION_STATE(0) macros.
This changes things. FPU exceptions are “sticky,” meaning they accumulate as operations are performed in the VM. The “inexact” flag could be set by any previous instruction, which makes code much trickier to reason about.
Here is the full list of opcodes as named in the source code.
1typedef enum : s64 {
2 PUSH_CONST, POP, DUP, DUP2, DUP_X1, SWAP, NOP,
3 ADD, SUB, MUL, DIV, FLOOR, CEIL, TRUNC, ROUND, ABS, MIN, MAX,
4 CLEAR_EXCEPT, B_DIVBYZERO, B_INEXACT, B_INVALID, B_OVERFLOW, B_UNDERFLOW, B_ANY, B_ALWAYS,
5 CALL, RET,
6 PRINT_FLOAT, PRINT_CHAR, READ_FLOAT, READ_CHAR,
7 LOAD, STORE
8} insn_t;
About Floating Points
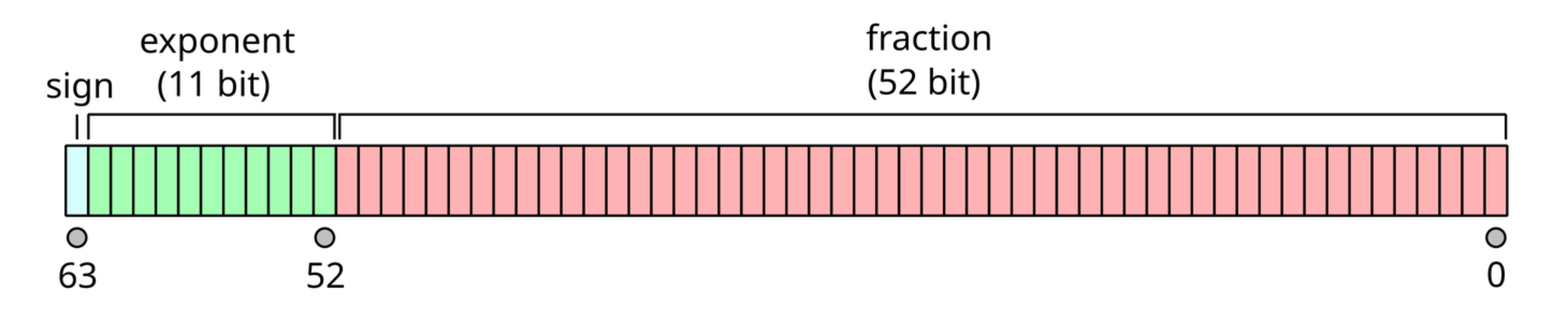
boat-vm specifically relies on the behavior of the C double datatype, which on our platform, corresponds to the
IEEE 754 double-precision binary floating-point format. A double includes a sign bit, an 11-bit biased exponent,
and a 52-bit mantissa which represents the fractional component of the significand.
The significand actually contains an implicit integer bit of value 1, which makes the total precision 53 bits. For a normal floating-point numbers, this formula is used to compute the real value:
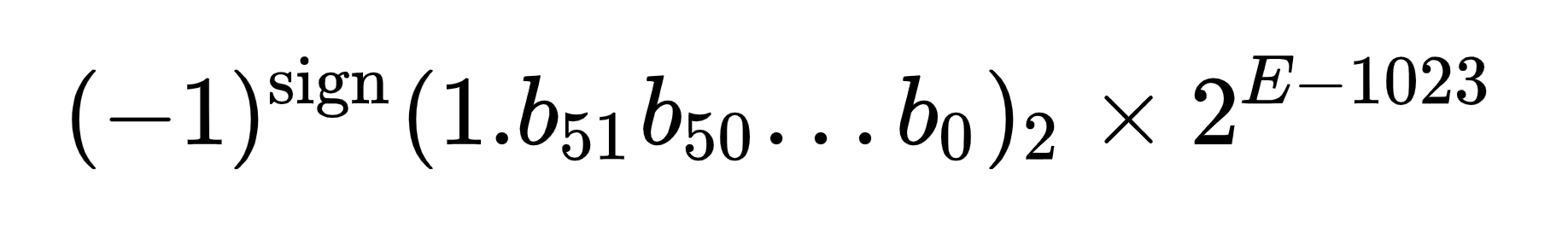
When the FPU cannot precisely represent the result of an arithmetic operation,
it will raise the INEXACT exception flag,
indicating the result. We can actually use this behavior to test the value of a floating point number: if a number is
greater than equal to one, its exponent value must be at least zero, and therefore its mantissa cannot represent an additional value 2^53. In my assembler, this algorithm is used to test whether numbers are greater than or equal to one:
1// function: return whether n greater than equal to 1
2int greaterThanOrEquals1Index = getProgramCount(buffer); // where the function starts
3System.out.println("linking greaterThanOrEquals1Index at pc " + greaterThanOrEquals1Index);
4buffer.putDouble(PUSH_CONST.encode()).putDouble(0.000042006942069)
5 .putDouble(MAX.encode()) // add minimum threshold to 1) make positive 2) prevent small magnitude errors
6 .putDouble(PUSH_CONST.encode()).putDouble(makeDouble(false, -53, 0))
7 .putDouble(CLEAR_EXCEPT.encode())
8 .putDouble(ADD.encode()) // n + 2^(-53) is inexact if n >= 1 due to exponent
9 .putDouble(POP.encode()) // we didn't need the result, only the fpu flags
10 .putDouble(PUSH_CONST.encode()).putDouble(1)
11 .putDouble(PUSH_CONST.encode()).putDouble(0) // 1, 0
12 .putDouble(B_INEXACT.encode()).putDouble(2) // skip 2 instructions if inexact
13 .putDouble(SWAP.encode()) // 0, 1
14 .putDouble(POP.encode()) // if inexact, keep 1, else keep 0
15 .putDouble(RET.encode());
Similarly, when the magnitude of a floating-point computation overflows past the maximum possible real value into infinity, the OVERFLOW exception flag is set. When we divide the maximum possible real double value by any number less than one, the computation will overflow. By using the sticky property of FPU flags, we can divide that special number by
both a number and its reciprocal, raising no exceptions only when the input number is exactly one.
This is how my program implements that algorithm to check for strict equality to the value 1.0:
1// function: return whether n is exactly equal to 1
2int equals1Index = getProgramCount(buffer); // where the function starts
3System.out.println("linking equals1Index at pc " + equals1Index);
4// we need to normalize our value to check if *exactly* 1
5buffer.putDouble(PUSH_CONST.encode()).putDouble(0.000042006942069)
6 .putDouble(MAX.encode()) // add minimum threshold to make positive
7 .putDouble(PUSH_CONST.encode()).putDouble(Double.MAX_VALUE)
8 .putDouble(SWAP.encode()) // max_value, n
9 .putDouble(DUP2.encode()) // max_value, n, max_value, n
10 .putDouble(PUSH_CONST.encode()).putDouble(1) // max_value, n, max_value, n, 1
11 .putDouble(SWAP.encode())
12 .putDouble(DIV.encode()) // max_value, n, max_value, 1/n
13 .putDouble(CLEAR_EXCEPT.encode()) // fire incoming !!!!!!!!!!!
14 .putDouble(DIV.encode()) // raises fpu exception if 1/n < 1
15 .putDouble(POP.encode())
16 .putDouble(DIV.encode()) // raises fpu exception if n < 1
17 .putDouble(POP.encode())
18 .putDouble(B_OVERFLOW.encode()).putDouble(3); // implied OR gate because FPU exception flags are sticky
19
20// no exception case: n == 1
21buffer.putDouble(PUSH_CONST.encode()).putDouble(1)
22 .putDouble(RET.encode());
23
24// overflow exception: n != 1
25buffer.putDouble(PUSH_CONST.encode()).putDouble(0)
26 .putDouble(RET.encode());
With these basic primitives covered, we can go about implementing the full challenge program.
The Program
Uncreatively, I decided to make the flag computer program solve a sudoku problem in order to decode the flag. At the time, I couldn’t think of any other interesting problems that could be implemented in a very inefficient way.
The program contained a function to load a hard-coded sudoku puzzle into the memory addresses 0-81, as well as a lookup table around the address 100 which would translate the sudoku keys into prime numbers which could be multiplied together to verify their correctness. You can think of it as a kind of check-product for each constraint on the board.
1// function: init puzzle
2int initPuzzleIndex = getProgramCount(buffer);
3String puzzle = ".......1.4.........2...........5.4.7..8...3....1.9....3..4..2...5.1........8.6...";
4// for faster solve, use "....84512487512936125963874932651487568247391741398625319475268856129743274836159";
5for (int i = 0; i < puzzle.length(); i++) {
6 char c = puzzle.charAt(i);
7 if (c == '.') {
8 buffer.putDouble(PUSH_CONST.encode()).putDouble(-1.0); // push -1 for empty cell
9 } else {
10 buffer.putDouble(PUSH_CONST.encode()).putDouble((double) (c - '0')); // push digit
11 }
12} // load entire puzzle into stack
13buffer.putDouble(PUSH_CONST.encode()).putDouble(puzzle.length()); // push puzzle length
14
15// loop start: check if TOS is 0; if so, break the loop
16buffer.putDouble(DUP.encode())
17 .putDouble(PUSH_CONST.encode()).putDouble(1)
18 .putDouble(SWAP.encode()) // n, 1, n
19 .putDouble(CLEAR_EXCEPT.encode()) // clear fpu exceptions
20 .putDouble(DIV.encode()) // calculate 1 / n, see if it gives div by 0 error
21 .putDouble(POP.encode()) // n
22 .putDouble(B_DIVBYZERO.encode()).putDouble(6); // skip to end of loop
23
24// loop body
25buffer.putDouble(PUSH_CONST.encode()).putDouble(-1)
26 .putDouble(ADD.encode()) // decrement index
27 .putDouble(DUP_X1.encode()) // index, val, index
28 .putDouble(STORE.encode()) // store the val at index
29 .putDouble(B_ALWAYS.encode()).putDouble(-11); // jump to top of loop
30
31// loop end
32buffer.putDouble(POP.encode()); // pop the index
33
34// set up lookup table
35int[] primeNumbers = new int[] { 2, 3, 5, 7, 11, 13, 17, 19, 23 };
36for (int i = 0; i < primeNumbers.length; i++) {
37 buffer.putDouble(PUSH_CONST.encode()).putDouble((double) primeNumbers[i])
38 .putDouble(PUSH_CONST.encode()).putDouble(100 + i + 1) // push prime number and its index
39 .putDouble(STORE.encode()); // store it in the lookup table
40}
41// lookup for -1 cell: garbage value
42buffer.putDouble(PUSH_CONST.encode()).putDouble(-0.0000000000042069)
43 .putDouble(PUSH_CONST.encode()).putDouble(99) // push prime number and its index
44 .putDouble(STORE.encode()); // store it in the lookup table
45
46buffer.putDouble(RET.encode()); // return from initPuzzle function
Then, I made the functions to check whether the board had been solved for each required row, column, and 3x3 square. For brevity, I’ll only show the final, overall function, which combines them together:
1// function: check solution
2// for each set of 9 cells, look up into primes and compute product
3// then divide that product by 223092870, the intended product
4// then, we get a ratio that represents whether it solved correctly
5// multiply all those ratios for each set and see if it >= 1 using that function.
6int checkSolutionIndex = getProgramCount(buffer);
7System.out.println("linking checkSolutionIndex at pc " + checkSolutionIndex);
8buffer.putDouble(PUSH_CONST.encode()).putDouble(9); // loop from range (0,9)
9
10// loop start: check if TOS is less than 1; if so, break the loop
11buffer.putDouble(DUP.encode())
12 .putDouble(CALL.encode()).putDouble(greaterThanOrEquals1Index) // check if i >= 1
13 .putDouble(PUSH_CONST.encode()).putDouble(1) // i, bool, 1
14 .putDouble(SWAP.encode()) // i, 1, bool
15 .putDouble(CLEAR_EXCEPT.encode()) // clear fpu exceptions
16 .putDouble(DIV.encode()) // calculate 1 / bool, see if it gives div by 0 exception
17 .putDouble(POP.encode()) // i
18 .putDouble(B_DIVBYZERO.encode()).putDouble(13); // skip to end of loop if i < 1
19
20// loop body: decrement i and compute check-products
21buffer.putDouble(PUSH_CONST.encode()).putDouble(1)
22 .putDouble(SUB.encode()) // i--
23 .putDouble(DUP.encode())
24 .putDouble(CALL.encode()).putDouble(getRowProductIndex)
25 .putDouble(SWAP.encode())
26 .putDouble(DUP.encode())
27 .putDouble(CALL.encode()).putDouble(getColumnProductIndex)
28 .putDouble(SWAP.encode())
29 .putDouble(DUP.encode())
30 .putDouble(CALL.encode()).putDouble(getSquareProductIndex)
31 .putDouble(SWAP.encode())
32 .putDouble(B_ALWAYS.encode()).putDouble(-19); // jump to top of loop
33
34// loop end
35buffer.putDouble(POP.encode());
36
37// multiply all the check-products !!
38buffer.putDouble(PUSH_CONST.encode()).putDouble(1.0);
39for (int i=0; i<27; i++) {
40 buffer.putDouble(MUL.encode());
41}
42
43// we need to normalize our value to check if *exactly* 1
44buffer.putDouble(CALL.encode()).putDouble(equals1Index)
45 .putDouble(RET.encode());
Finally, I had to make the algorithm to solve the sudoku. On the VM, I implemented a simple recursive
backtracking algorithm, which recursively attempts guesses for each unfilled square in the puzzle until the problem
is solved. The base case for when index == 81 simply checks whether the board has been successfully solved.
Note the use of the DIVBYZERO flag in order to break the loop.
1// function: attempt_solve_recursive(index)
2// recursively brute forces the solver with index++ until index == 81.
3// where it does a final check and returns boolean
4int attemptSolveRecursiveIndex = getProgramCount(buffer);
5System.out.println("linking attemptSolveRecursiveIndex at pc " + attemptSolveRecursiveIndex);
6// if index == 81, simply do a check and return
7buffer.putDouble(DUP.encode()) // index, index
8 .putDouble(PUSH_CONST.encode()).putDouble(81) // index, index, 81
9 .putDouble(DIV.encode()) // index, index/81
10 .putDouble(CALL.encode()).putDouble(equals1Index) // check if index == 81
11 .putDouble(PUSH_CONST.encode()).putDouble(1)
12 .putDouble(SWAP.encode()) // index, 1, bool
13 .putDouble(CLEAR_EXCEPT.encode())
14 .putDouble(DIV.encode())
15 .putDouble(POP.encode()) // we dont need result, just the exception flag
16 .putDouble(B_DIVBYZERO.encode()).putDouble(4); // skip branch if not index == 81
17
18// base case: just check if solved and return result (also pop the index)
19buffer.putDouble(POP.encode())
20 .putDouble(CALL.encode()).putDouble(checkSolutionIndex)
21 .putDouble(RET.encode());
22
23// otherwise, do recursive guessing
24// first, check if the cell is empty (< 1)
25buffer.putDouble(DUP.encode()) // index, index
26 .putDouble(LOAD.encode()) // index, curr_val
27 .putDouble(CALL.encode()).putDouble(greaterThanOrEquals1Index) // check if i >= 1
28 .putDouble(PUSH_CONST.encode()).putDouble(1) // index, bool, 1
29 .putDouble(SWAP.encode()) // index, 1, bool
30 .putDouble(CLEAR_EXCEPT.encode())
31 .putDouble(DIV.encode())
32 .putDouble(POP.encode()) // we dont need result, just the exception flag
33 .putDouble(B_DIVBYZERO.encode()).putDouble(5); // skip branch if i still needs guessing; // index
34
35// case: there is already a hint at this cell
36// just recurse next without guesses and return that result
37buffer.putDouble(PUSH_CONST.encode()).putDouble(1)
38 .putDouble(ADD.encode())
39 .putDouble(CALL.encode()).putDouble(attemptSolveRecursiveIndex) // recurse (index + 1)
40 .putDouble(RET.encode());
41
42// regular case: make guesses [1, 9], break loop if returned true
43buffer.putDouble(PUSH_CONST.encode()).putDouble(9); // index, guess
44
45// loop start: check if guess is still >= 1
46buffer.putDouble(DUP.encode()) // index, guess, guess
47 .putDouble(CALL.encode()).putDouble(greaterThanOrEquals1Index) // check if guess >= 1
48 .putDouble(PUSH_CONST.encode()).putDouble(1) // index, guess, bool, 1
49 .putDouble(SWAP.encode()) // index, guess, 1, bool
50 .putDouble(CLEAR_EXCEPT.encode())
51 .putDouble(DIV.encode())
52 .putDouble(POP.encode()) // we dont need result, just the exception flag
53 .putDouble(B_DIVBYZERO.encode()).putDouble(22); // break loop if guess is zero now; // index, guess
54
55// loop body: attempt guess and then decrement index
56buffer.putDouble(DUP2.encode()) // index, guess, index, guess
57 .putDouble(SWAP.encode()) // index, guess, guess, index
58 .putDouble(STORE.encode()) // index, guess
59 .putDouble(SWAP.encode()) // guess, index
60 .putDouble(DUP_X1.encode()) // index, guess, index
61 .putDouble(PUSH_CONST.encode()).putDouble(1)
62 .putDouble(ADD.encode()) // index, guess, index + 1
63 .putDouble(CALL.encode()).putDouble(attemptSolveRecursiveIndex) // recurse (index + 1); puts a bool on tos
64 .putDouble(PUSH_CONST.encode()).putDouble(1) // index, guess, bool, 1
65 .putDouble(SWAP.encode()) // index, guess, 1, bool
66 .putDouble(CLEAR_EXCEPT.encode())
67 .putDouble(DIV.encode())
68 .putDouble(POP.encode()) // we dont need result, just the exception flag
69 .putDouble(B_DIVBYZERO.encode()).putDouble(5); // skip this if guess failed; // index, guess
70
71// success! we're done now
72// pop index, guess; return 1
73buffer.putDouble(POP.encode())
74 .putDouble(POP.encode())
75 .putDouble(PUSH_CONST.encode()).putDouble(1) // true
76 .putDouble(RET.encode());
77
78// otherwise, the guess didn't work. we need to decrement guess and loop again
79buffer.putDouble(PUSH_CONST.encode()).putDouble(-1) // index, guess, -1
80 .putDouble(ADD.encode()) // guess--
81 .putDouble(B_ALWAYS.encode()).putDouble(-28);
82
83// loop end
84// all guesses failed; return false
85// restore the value as -1 at index
86// pop index, guess; return 0
87buffer.putDouble(POP.encode()) // index
88 .putDouble(PUSH_CONST.encode()).putDouble(-1) // index, -1
89 .putDouble(SWAP.encode()) // -1, index
90 .putDouble(STORE.encode()) // memory[index] = -1
91 .putDouble(PUSH_CONST.encode()).putDouble(0) // false
92 .putDouble(RET.encode());
Finally, we make an entry function which starts the recursive chain.
1// function: attempt_solve() returns whether it worked
2int attemptSolveIndex = getProgramCount(buffer);
3System.out.println("linking attemptSolveIndex at pc " + attemptSolveIndex);
4buffer.putDouble(PUSH_CONST.encode()).putDouble(0)
5 .putDouble(CALL.encode()).putDouble(attemptSolveRecursiveIndex) // call algorithm starting with 0
6 .putDouble(RET.encode());
If you think that I must be insane for implementing my own recursive sudoku solver in my own made-up floating-point assembly language, you’re probably right.
After solving the sudoku, we hash the board in order to generate the flag using a simple multiply-and-add algorithm.
1// function: hash_board() loops through the board and returns a hash
2// loops through from index 0 to 81, multiplying and adding
3int hashBoardIndex = getProgramCount(buffer);
4System.out.println("linking hashBoardIndex at pc " + hashBoardIndex);
5buffer.putDouble(PUSH_CONST.encode()).putDouble(0.00000000069) // seed value
6 .putDouble(PUSH_CONST.encode()).putDouble(200) // memory address
7 .putDouble(STORE.encode()) // memory[200] = 0.00000000069, used for hash
8 .putDouble(PUSH_CONST.encode()).putDouble(0); // loop from 0 to 81
9
10// loop start: check if TOS is greater than or equals 81; if so, break the loop
11buffer.putDouble(DUP.encode())
12 .putDouble(PUSH_CONST.encode()).putDouble(81)
13 .putDouble(DIV.encode())
14 .putDouble(CALL.encode()).putDouble(greaterThanOrEquals1Index) // check if i/81 >= 1
15 .putDouble(PUSH_CONST.encode()).putDouble(1) // i, bool, 1
16 .putDouble(SWAP.encode()) // i, 1, bool
17 .putDouble(SUB.encode()) // i, !bool
18 .putDouble(PUSH_CONST.encode()).putDouble(1) // i, !bool, 1
19 .putDouble(SWAP.encode()) // i, 1, !bool
20 .putDouble(CLEAR_EXCEPT.encode())
21 .putDouble(DIV.encode())
22 .putDouble(POP.encode()) // we dont need result, just the exception flag
23 .putDouble(B_DIVBYZERO.encode()).putDouble(17); // break loop if i/81 >= 1 is true
24
25// loop body: hash the current board state
26buffer.putDouble(DUP.encode())
27 .putDouble(LOAD.encode()) // i, memory[i]
28 .putDouble(PUSH_CONST.encode()).putDouble(200)
29 .putDouble(DUP_X1.encode())
30 .putDouble(LOAD.encode()) // i, 200, memory[i], memory[200]
31 .putDouble(PUSH_CONST.encode()).putDouble(Math.PI)
32 .putDouble(MUL.encode()) // i, 200, memory[i], memory[200] * Math.PI
33 .putDouble(SWAP.encode()) // i, 200, memory[200] * Math.PI, memory[i]
34 .putDouble(MUL.encode()) // i, 200, memory[200] * Math.PI * memory[i]
35 .putDouble(PUSH_CONST.encode()).putDouble(Math.E)
36 .putDouble(ADD.encode()) // i, 200, memory[200] * Math.PI * memory[i] + e
37 .putDouble(SWAP.encode()) // i, new_hash, 200
38 .putDouble(STORE.encode()) // store new_hash in memory[200]
39 .putDouble(PUSH_CONST.encode()).putDouble(1) // i, 1
40 .putDouble(ADD.encode()) // i + 1
41 .putDouble(B_ALWAYS.encode()).putDouble(-28); // jump back to loop start
42
43// loop end
44buffer.putDouble(PUSH_CONST.encode()).putDouble(200)
45 .putDouble(LOAD.encode())
46 .putDouble(RET.encode());
Finally, the program prints the flag. Many teams analyzed the hardcoded
printed characters in the program, obtaining the incorrect flag corctf{g3ntly_d0wn_th3_StR3AM_FPU_h4cks}
without noticing the crucial PRINT_FLOAT instruction in the middle,
which prints the hash of the board. This is what the program actually does:
1buffer.putDouble(CALL.encode()).putDouble(hashBoardIndex); // call hashBoard function
2printString(buffer, "\nFlag: \n");
3printString(buffer, "corctf{g3ntly_d0wn_th3_StR3AM_");
4buffer.putDouble(PRINT_FLOAT.encode()); // prints the board hash
5printString(buffer, "FPU_h4cks}\n");
6printString(buffer, "\nThank you for your patience!\n");
One way to obtain the flag is to solve the sudoku and then reïmplement the hash function. This is what my python solver looked like:
1BOARD_PROBLEM = ".......1.4.........2...........5.4.7..8...3....1.9....3..4..2...5.1........8.6..."
2
3def board_hash(board):
4 """Compute a hash of the board state."""
5 hash = 0.00000000069 # seed
6 for row in board:
7 for val in row:
8 hash = hash * math.pi * float(val) + math.e
9 return hash
10
11if __name__ == '__main__':
12 test()
13 solve_all([BOARD_PROBLEM], "custom", 0) # just for the display lol
14
15 values = to_array(solve(BOARD_PROBLEM))
16 solution_string = "".join("".join(str(n) for n in row) for row in values)
17 print(f"Original: {BOARD_PROBLEM}")
18 print(f"Solution: {solution_string}")
19 print()
20
21 hash = board_hash(values)
22 # flag format: corctf{g3ntly_d0wn_th3_StR3AM_<hash>FPU_h4cks}
23 flag = f"corctf{{g3ntly_d0wn_th3_StR3AM_{hash}FPU_h4cks}}"
24 print(f"Hash of the solution: {flag}")
25 print()
26
27 print(f"flag: ")
Another solution was to patch the bytecodes hard-coding the sudoku, replacing it with the full solution
and running the program again to immediately print the flag. And this time, it won’t take
2.2185312001337001e+57 seconds to get the flag
corctf{g3ntly_d0wn_th3_StR3AM_3.0390693652230334e+89FPU_h4cks}.
The CTF
From what I can understand, the patching approach was the most viable approach to solving the challenge.
Many teams tried to emulate the VM’s behavior in python, but could only crudely approximate the
INEXACT logic by hand. In any case, players had to work out what algorithm was running and solve the
puzzle externally in order to speed up the program.
We received an insane amount of questions about this challenge because many teams found the plaintext of the
flag template corctf{g3ntly_d0wn_th3_StR3AM_FPU_h4cks} without solving for the middle part,
which would have produced the correct corctf{g3ntly_d0wn_th3_StR3AM_3.0390693652230334e+89FPU_h4cks} if
the given program were theoretically run to completion. I’m not entirely sure how I can design the flag
or program to not look like a confusing decoy, but next time I’ll try to make it more obvious, maybe by
splitting the text into even more parts.
During the full 48-hour CTF competition, 13 teams were able to solve this challenge,
making whatever-floats-your-boat one of the harder rev challenges for corCTF 2025. Despite using such an obscure
concept for the VM, the actual operations were fairly simple to analyze as the control flow jump offsets
were clearly defined, and the VM contained a clear data and call stack. Solvers could often infer what the
program was doing via some basic static analysis and intuition. For future challenges, I could probably
obfuscate the raw data of the puzzle a little bit more, so that players don’t just see things like
“this program loads 81 numbers 1-9” or use a more niche algorithm which had to be fully understood
in order to get the correct flag.
The Conclusion
Although boat-vm doesn’t have clear instructions for boolean logic and value comparison, with some
clever tricks, we can create efficient floating-point algorithms to control our code.
In the end, the explicit, contained control flow of the VM made this challenge
manageable for many participants.
I absolutely loved making this challenge and learning about IEEE 754 floating-point arithmetic. Although I didn’t realize what it had meant when I got assigned for corCTF a few months ago, reverse engineering turned out to be a great way to explore computing as a whole. I hope to continue developing projects around niche and quirky concepts as a way to both challenge others and continue to learn myself.