corCTF 2025 - bubble-vm
- Author: maxster
- Date:
corCTF 2025 - bubble-vm
Hey, I’m also posting on this site now!
This was my first year writing CTF challenges, and I mainly focused on software reverse engineering. I absolutely enjoyed playing with various models of computation and seeing other people try to solve my problems.
In this blog, I will talk about the design choices and decisions behind this VM architecture and how I created this challenge.
The Virtual Machine
I love virtual machines.
According to my tallying, I invented four turing-complete systems for corCTF rev, and three of them were
VMs. Although each challenge had its own quirks, bubble-vm ended up being the hardest VM with only 2 solves
due to its obscure data manipulation and control flow tactics.
Having little prior experience with CTFs, I had no clue what types of challenges to write for corCTF 2025. I wanted to push myself by making an advanced challenge, and I found out that writing custom architectures was a potential way to isolate a challenge from existing analysis tools. I ended up stretching this idea in several different ways for this CTF, dabbling with all sorts of models of computation across three different challenge categories.
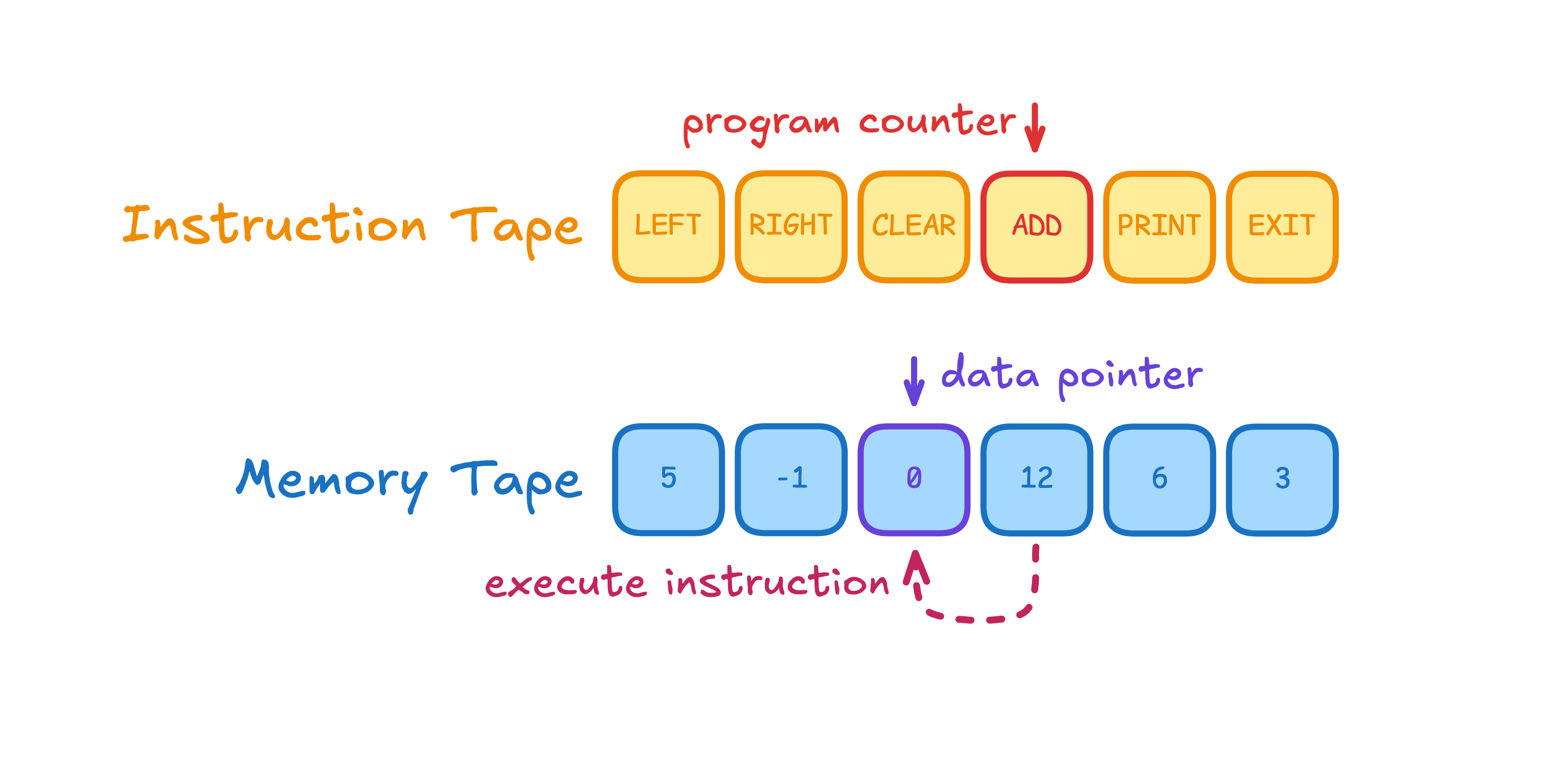
This challenge is a testament to how complex program logic can emerge from a very simple and limited set of instructions. Borrowing from the BF programming language, the machine had only two pointers operating on two tapes: a program counter, which dictates interpretation over an immutable instruction buffer, and a data pointer, which allows operations on a large tape of 64-bit integers. Additionally, each instruction was encoded with a single character which couldn’t contain any metadata.
In order to facilitate more advanced computations, the instruction set also contained several binary operations
that operated with the data in the next cell — for example, the ADD instruction writes the sum of
data[A] and data[A+1] into data[A]. The BUBBLE instruction, from which the VM derives its name,
swaps the data in the current and next data cell, similar to a bubble sort.
As you can probably imagine, most bytecodes in this system are very standard and
are straightforward to analyze.
What made this challenge hard was the way the VM enabled random access along its instruction and memory tape.
The VM contained two perculiar instructions which manipulated the program state in oddly specific ways:
the SHIFT instruction would move the data pointer to the value stored in data[A] and copy
the value stored in the previous neighbor data[A+1] into the new location,
and the JUMP instruction would set the program count to the value stored in data[A] and write back
into the same cell the successor of the original program count. If that sounds confusing, just
remember that I had to write an entire 10,000-bytecode program using this system using my own assembler.
Here is the (sloppy) internal documentation of the bytecodes for bubble-vm:
1/*
2 * The VM is made of a linear memory space of cells which are addressable via indexing.
3 * The VM has one register: a cell pointer A, which is used to calculate the A+1 pointer.
4 *
5 * The program starts with A pointing to the cell at index 0.
6 * Cell 0 is initially set to the length of the cell buffer, and all other cells are cleared.
7 *
8 * Instruction set:
9 * BUBBLE - swap values at A and A+1
10 * TAKE - set A to A+1 value
11 * LEFT, RIGHT - decrement/increment A pointer
12 * BZ, BNZ - relative branch by numerical value in A if A+1 is zero/nonzero
13 * ADD, SUB, MUL, DIV, MOD - do integer operation on A and A+1 and store result in A
14 * SLL, SRL, SRA, XOR, AND, OR - do integer operation on A and A+1 and store result in A
15 * NONZERO - set cell A to 1 if A is nonzero, 0 otherwise (convert int to boolean 1/0)
16 * NOT - flip bits of A
17 * INC, DEC - increment/decrement the numerical value of A
18 * CLEAR - set cell A to zero
19 * INPUT - reads a char to A
20 * PRINT - outputs A as char
21 * EXIT - halt program and exit
22 * IDENTITY - store cell address of A in A
23 * SHIFT - shift to A and write prev A+1 value (copies A+1 to target address)
24 * JUMP - jump to A and write prev next instruction address (return address)
25 */
The Control Primitives
Remember those obscure SHIFT and JUMP instructions? As it turns out,
these instructions serve critical roles in managing the logic of the VM.
The JUMP opcode always writes back a return address, and is therefore ideal for emulating function calls.
Combining this with the fact that most instructions operate on data to the right of the data pointer,
it naturally makes sense for programs to use a downwards-growing stack,
starting from the highest memory address and sliding left to obtain more space. When a function needs to return,
it will simply slide the data pointer back to where it started, and call the JUMP instruction on the return address,
returning control to the callee.
The SHIFT instruction, however, is trickier. It may seem quite bizzare and useless, since it can
only transport a single data value to the target location without an obvious way to return back to the
original position, but through a careful construction, we can enable arbitrary reads and writes to global
memory addresses from anywhere on the callstack. The key is to use a sparse, two-wide memory layout,
where load/store cells contain a temporary slot which can get overwritten, while the important data is stored in the
cell’s neighbor.
I won’t bore you with all the details. Here’s how I implemented the load and store primitives in my assembler:
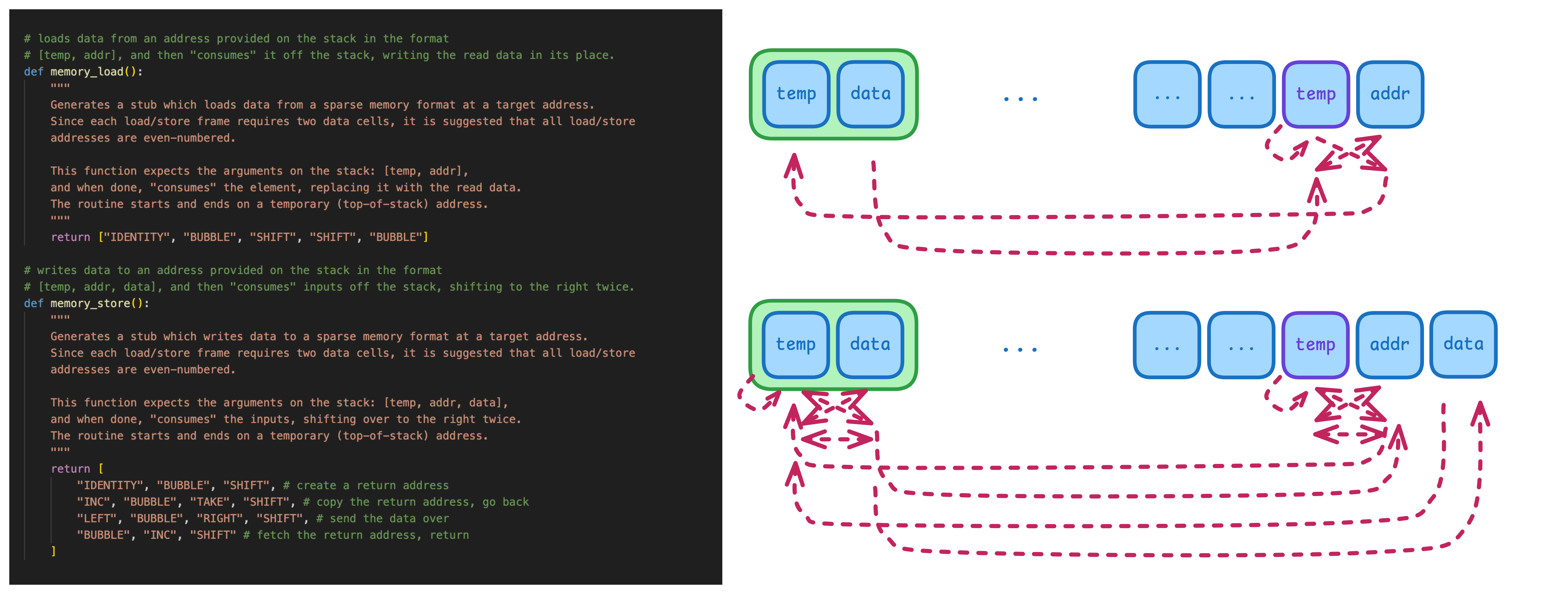
Using these two instructions, we can create a call stack and access global variables at any point in the program.
The Data Primitives
bubble-vm doesn’t have instructions to load immediate data into the program, so I wrote a macro in my
python assembler to create numbers using a bitmasking algorithm. The code first loads in the absolute value
because it tends to be more efficient for negative numbers. This function probably isn’t the most optimal way
to load in a number into the program, but it did the job.
1def u64_to_bitstring(num):
2 if num < 0:
3 raise ValueError("Cannot convert negative number to bits")
4 binary_string = bin(num) # format 0b1001
5 return binary_string[2:]
6
7# loads a number into a cell.
8# Use this when exact sizing is not critical, and there is space to the left.
9def load_number(num):
10 needs_negate = num < 0
11 unsigned_num = abs(num)
12
13 # algorithm: bitmask the absval, and then subtract from 0 if negative
14 prologue = ["CLEAR", "INC", "LEFT", "CLEAR", "INC", "LEFT", "CLEAR", "RIGHT"]
15 # sets up format [result, mask, 1], initially [0, 1, 1]
16 bitmask = []
17 for digit in u64_to_bitstring(unsigned_num)[::-1]:
18 if digit == '1':
19 bitmask += ["LEFT", "OR", "RIGHT"]
20 bitmask.append("SLL") # shift the mask bit to the left
21 pos_epilogue = ["LEFT", "BUBBLE", "RIGHT", "BUBBLE", "RIGHT"]
22 neg_epilogue = ["CLEAR", "LEFT", "BUBBLE", "SUB", "BUBBLE", "RIGHT", "BUBBLE", "RIGHT"]
23 epilogue = neg_epilogue if needs_negate else pos_epilogue
24
25 return prologue + bitmask + epilogue
The Control Flow, Part Two
The way the code loads numbers poses a problem to our control flow management. Functions must be called using a precise target address, but our VM doesn’t guarantee a fixed-length solution for loading numbers. This creates a nightmare for linking functions in our program — we would have to resolve a circular loop of dependencies between functions in order for the code to behave. This problem would be made even more annoying when a function call was made on a conditional branch, where the branch offset also required a precise offset calculation.
Rather than creating an overcomplicated symbol linker which solved the complex network of dependencies between objects in my code, I decided to make a jump table that would handle all the function offsets in a single location at the beginning of the program. This way, function callers would only need to load the index of the function they want to call, and jump to a fixed location for the dynamic dispatch.
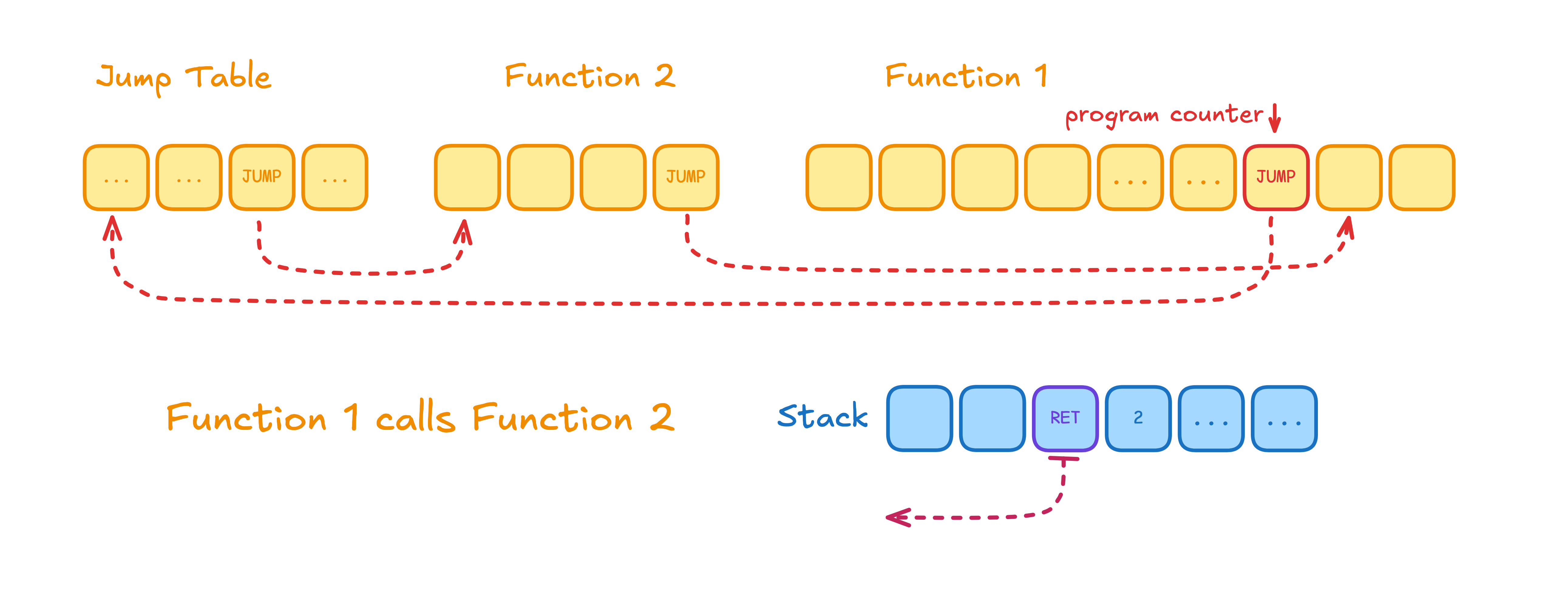
This ended up being my code for linking programs together. Although it is fairly cumbersome, it was much easier having this logic all in one place, rather than across the entire program.
1# Jump table: does a bunch of BZ and DEC insns
2def link_program():
3 prologue = ["BUBBLE", "RIGHT", "BUBBLE"] # the name of the VM!
4
5 # convention: [extra_space, ret_addr, idx, args] (idx missing on _start)
6 _start_impl = ["RIGHT", "RIGHT", "DEC", "SHIFT", *call_function("main"), "EXIT"]
7 jump_table_handler = [
8 "LEFT", "CLEAR", *["INC"] * len(_start_impl), "INC", "BNZ",
9 *_start_impl, # skip _start if ret addr exists
10 ]
11
12 relevant_functions = FUNCTIONS[1:]
13
14 for funct_name in relevant_functions:
15 if funct_name not in CALLED_FUNCTIONS:
16 print(f"Warning: function {funct_name} is linked in program but not called anywhere")
17
18 function_impls = [FUNCTION_IMPLEMENTATIONS[funct_name] for funct_name in relevant_functions]
19 function_lengths = [len(function_impl) for function_impl in function_impls]
20 function_offsets = [0]
21 for function_length in function_lengths[:-1]:
22 function_offsets.append(function_offsets[-1] + function_length)
23 function_data_segment = [insn for funct_impl in function_impls for insn in funct_impl]
24
25 jump_table_calculation_estimate = sum(
26 load_number_estimate(offset) + load_number_estimate(load_number_estimate(offset)) + 15
27 for offset in function_offsets
28 )
29 function_data_start = 50 + jump_table_calculation_estimate # assume this starts in a good location
30
31 # handle function jump table [extra_space, ret_addr, idx, args]
32 jump_table_handler += load_number(function_data_start) # [data_start, ret_addr, idx, args] at data_start
33 jump_table_handler += [
34 "RIGHT", "BUBBLE", "LEFT", "BUBBLE" # bubble sort! drag idx back 2 spaces
35 ] # [extra_space, idx, data_start, ret_addr, args] at idx
36
37 for i in range(len(relevant_functions)):
38 funct_name = relevant_functions[i]
39 funct_offset = function_offsets[i]
40 # Original layout: [extra_space, idx, data_start, ret_addr, args] at idx
41 # Becomes at invocation: [offset, temp, idx, data_start, ret_addr, args] at temp
42 table_invoke = ["LEFT", "BUBBLE", "RIGHT", "BUBBLE", "RIGHT", "ADD", "BUBBLE", "RIGHT", "JUMP"]
43 funct_handler = [
44 "DEC", "LEFT", # decrease index, go to extra space
45 *load_number(funct_offset), # [offset, idx, data_start, ret_addr, args] at offset
46 "LEFT", "TAKE", "RIGHT", # [offset, temp, idx, data_start, ret_addr, args] at temp
47 "CLEAR", *["INC"] * len(table_invoke), "INC", "BNZ", # [offset, skip_amount, idx, data_start, ret_addr, args]
48 *table_invoke, # add offset to data_start and invoke. skip this if not zero (not matched)
49 "RIGHT" # otherwise, go back and try next iteration
50 ]
51
52 jump_table_handler += funct_handler
53
54 # if no function found, panic, print something, and exit
55 jump_table_handler += [
56 "NOP",
57 "CLEAR", "INC", "INC", "INC", "INC", "SHIFT", # go to somewhere safe
58 *load_number(101), # ASCII 'e'
59 "PRINT", "PRINT", "PRINT", "EXIT"
60 ]
61
62 def get_padding_insn(i):
63 # return "EXIT"
64 choice_list = list(INSNS.keys())
65 return choice_list[(i * 5 + 5 * i ** 3 + 16 - i ** 2) % len(choice_list)]
66
67 padding = [get_padding_insn(i) for i in range(function_data_start - len(jump_table_handler) - len(prologue))]
68
69 beginning_length = len(prologue) + len(jump_table_handler) + len(padding)
70 for funct_name in relevant_functions:
71 funct_impl = FUNCTION_IMPLEMENTATIONS[funct_name]
72 funct_len = len(funct_impl)
73 print(f"linking {funct_name} at program count {beginning_length} - {beginning_length + funct_len}")
74 beginning_length += funct_len
75
76 return prologue + jump_table_handler + padding + function_data_segment
With this system, as long as a function was declared beforehand, it could be called from anywhere, and there would not be any additional constraints during linkage. As a result, we are able to write very complex programs supporting function calls, recursion, global variables, and more using a very simple bytecode architecture.
The Program
The actual program running on the VM was a flag verifier that requested a flag corctf{...} with a body
of 36 characters. As those characters were read, they were processed through a pseudorandom algorithm which would
scramble the case of the letters:
1
2HASH_MULTIPLIER = 13
3HASH_SEED = 0xDEADBEEF # as a long (+3735928559)
4
5define_function("init_hash", [
6 *load_number(HASH_MULTIPLIER), "LEFT", *load_number(148), "LEFT",
7 *memory_store(), # store multiplier at 148
8 *load_number(HASH_SEED), "LEFT", *load_number(146), "LEFT", # store seed at 146
9 *memory_store(), # store seed as hash state
10 "RIGHT", "JUMP" # return
11])
12
13# recursively calls until num_iter is zero
14define_function("update_hash_inner", [ # [ret_addr, temp, num_iter, data]
15 "BUBBLE", "RIGHT", "TAKE", "LEFT", "BUBBLE", "LEFT", "BUBBLE",
16 "RIGHT", "BUBBLE", "RIGHT", "BUBBLE", "RIGHT", "TAKE", "LEFT", "BUBBLE", "LEFT", "BUBBLE",
17 # [num_iter, data, ret_addr] args copied over, at data
18 "LEFT", "LEFT", *load_number(5), "BNZ", # [temp, num_iter, data, ret_addr] at temp
19 "RIGHT", "RIGHT", "RIGHT", "JUMP", # skip if num_iter is nonzero; return if zero
20 *load_number(148), "BUBBLE", *memory_load(), # [temp, hash_multiplier, data, ret_addr]
21 *load_number(146), "LEFT", *memory_load(), # [temp, old_state, hash_multiplier, data, ret_addr]
22 "RIGHT", "MUL", "BUBBLE", "RIGHT", "ADD", "BUBBLE", # [temp, new_state, ret_addr]
23 *load_number(146), "LEFT", *memory_store(), # store new state at 146
24 "BUBBLE", "RIGHT", "TAKE", "LEFT", "BUBBLE", "LEFT", "BUBBLE",
25 "RIGHT", "BUBBLE", "RIGHT", "BUBBLE", "RIGHT", "TAKE", "LEFT", "BUBBLE", "LEFT", "BUBBLE",
26 # [num_iter, data, ret_addr] args copied over, at data
27 "LEFT", "DEC", "LEFT", # [temp, num_iter - 1, data, ret_addr] at temp
28 *call_function("update_hash_inner"), # recursive call (no tail-call optimization)
29 "RIGHT", "RIGHT",
30 "RIGHT", "JUMP" # return from function
31])
32
33# updates the hash with the data five times
34define_function("update_hash", [ # [ret_addr, data]
35 "BUBBLE", "RIGHT", "TAKE", "LEFT", "BUBBLE", # pull function arg behind return address on stack
36 "LEFT", "CLEAR", *["INC"] * 5, "LEFT", # [temp, num_iter, data, ret_addr] at temp
37 *call_function("update_hash_inner"), # call inner recursive function
38 "RIGHT", "RIGHT",
39 "RIGHT", "JUMP" # return from function
40])
41
42define_function("get_hash", [
43 *load_number(146), "LEFT", *memory_load(), "RIGHT", # load hash state from 146
44 "BUBBLE", "RIGHT", "BUBBLE", "LEFT", "BUBBLE", # put result behind return address
45 "RIGHT", "JUMP" # return from function
46])
47
48# flips the upper/lower case of a character depending on the hash value
49define_function("get_char_scramble", [
50 "LEFT", *call_function("get_hash"), # [temp, hash_value] at temp
51 *load_number(32), "BUBBLE", "SRL", # [hash_value >> 32, _]
52 "BUBBLE", "CLEAR", *["INC"] * 2, "BUBBLE", "MOD",
53 "INC", "INC", "INC", "INC", "MOD", # normalize to 0 or 1
54 "BUBBLE", "LEFT", *load_number(0x20), "LEFT", "INPUT", # [input, 0x20, _, bool]
55 "LEFT", *call_function("update_hash"), "RIGHT",
56 "RIGHT", "RIGHT", "CLEAR", *["INC"] * 6, "BZ", # [input, 0x20, skip_offset, bool] at skip_offset
57 "LEFT", "LEFT", "XOR", "RIGHT", "RIGHT", # skip if zero
58 "LEFT", "LEFT", "BUBBLE", "RIGHT", "BUBBLE", # [temp, scrambled_input, _, ret_addr]
59 "RIGHT", "BUBBLE", "RIGHT", "BUBBLE", "RIGHT", "BUBBLE", "LEFT", "BUBBLE", # [temp, ret_addr, scrambled_input]
60 "RIGHT", "JUMP" # return from function
61])
The code performs a loop which iterates 36 times, processing the character through the scrambler and then encoding it into a number in a 6x6 matrix:
1#ahaHa
2# 0: a (97)
3# 1: h (104)
4# -1: H (72)
5# 5: everything else (bad)
6# [temp, _, addr, _, _, _, 72, 32] at temp
7read_and_store = [
8 *call_function("get_char_scramble"), "RIGHT",
9 *["BUBBLE", "RIGHT"] * 4, *["LEFT"] * 4, "BUBBLE", # [_, temp, addr, _, _, scrambled_input, 72, 32] at temp
10 "RIGHT", "RIGHT", "CLEAR", *["INC"] * 5, "RIGHT", "RIGHT",
11 "SUB", # subtract 72. Should be zero if 'H'
12 # "CLEAR", # : forces it to set to 'H' and -1 override
13 # "RIGHT", "PRINT", "LEFT", # santity check. hope this is actually an H
14 "LEFT", "CLEAR", *["INC"] * 9, "BNZ",
15 "LEFT", *["DEC"] * 6, "RIGHT", # skip this if nonzero
16 "RIGHT", "RIGHT", "BUBBLE", "LEFT", "SUB", # sub another 32. Should be zero if 'h'
17 "RIGHT", "BUBBLE", "LEFT", # restore the [72, 32]
18 "LEFT", "CLEAR", *["INC"] * 7, "BNZ",
19 "LEFT", *["DEC"] * 4, "RIGHT", # skip this if nonzero
20 "RIGHT", *["INC"] * 7, # add 7. Should be zero if 'a'
21 "LEFT", "CLEAR", *["INC"] * 8, "BNZ",
22 "LEFT", *["DEC"] * 5, "RIGHT", # skip this if zero
23 "LEFT", # [temp, temp, temp, addr, num, _, _, 72, 32] at num
24 "LEFT", "LEFT", "TAKE", "LEFT", "BUBBLE", # [temp, addr_copy, temp, addr, num, _, 72, 32]
25 "RIGHT", "RIGHT", "BUBBLE", "LEFT", "TAKE",
26 "RIGHT", "BUBBLE", "LEFT", # [temp, addr_copy, num_copy, addr, num, _, 72, 32] at num_copy
27 #"CLEAR", *["INC"] * 1, # TODO REMOVE THIS, SET TO 5 FORCEFULLY
28 "LEFT", "LEFT", *memory_store(), # [temp, addr, num, _, 72, 32] at temp
29 "RIGHT", "INC", "INC", "LEFT", *load_number(144), "SUB", # increment address (twice), compare
30 "LEFT"
31]
32
33read_and_store += load_back_branch_offset(len(read_and_store))
34read_and_store.append("BNZ") # keep looping until we reach the end
35
36define_function("read_input_as_b", [
37 *flatten(
38 [*load_number(ord(c)), "PRINT"]
39 for c in "Flag Verifier\nEnter flag in this format:\ncorctf{36_ascii_chars_inside___}\n"
40 ),
41 *["INPUT"] * len("corctf{"), # dispose of first 7 characters
42 *load_number(32), "LEFT", *load_number(72),
43 "LEFT", "LEFT", "LEFT", "LEFT", *load_number(72),
44 "LEFT", "LEFT", # [temp, _, addr, _, _, _, 72, 32] at temp
45 *read_and_store, # loops until done, at same register location
46 "INPUT", # consume closing brace }
47 "RIGHT", "RIGHT", "RIGHT", "RIGHT", "RIGHT", "RIGHT", "RIGHT",
48 *flatten(
49 [*load_number(ord(c)), "PRINT"]
50 for c in "\nChecking flag...\n"
51 ),
52 "RIGHT", "JUMP", # go back to return address and return
53])
The flag verifier required this encoded matrix to be the inverse of a given matrix:
1
2TARGET_MATRIX = [
3 0, 1, 0, 0, 0, 0,
4 1, 0, 1, 0, 0, 0,
5 0, 1, 0, 1, 0, 0,
6 0, 0, 1, 0, 1, 0,
7 0, 0, 0, 1, 0, 1,
8 0, 0, 0, 0, 1, 0,
9]
10
11define_function("load_matrix_a", [
12 "IDENTITY", "LEFT", "CLEAR", "SHIFT", # go to 0, transport return address
13 *flatten(
14 ["RIGHT", "CLEAR", *["INC"] * load_value, "RIGHT"]
15 for load_value in TARGET_MATRIX
16 ),
17 *flatten(["LEFT", "LEFT"] for load_value in TARGET_MATRIX),
18 "SHIFT", # initialized cells 0, 2, 4, ..., 70
19 "RIGHT", "JUMP" # return
20])
Finally, I put together the pieces of my program together, defining the main function:
1accept = call_function("accept_flag")
2reject = call_function("reject_flag")
3
4define_function("main", [
5 *call_function("init_hash"),
6 *call_function("load_matrix_a"),
7 *call_function("read_input_as_b"),
8 *call_function("mult_a_b_into_a"),
9 "LEFT", *call_function("reduce_a_bitwise_or"), # [temp, a, ret_addr] (a must be 1)
10 *call_function("mult_a_b_into_a"),
11 *call_function("a_sub_b"),
12 "LEFT", *call_function("reduce_a_bitwise_or"), # [temp, b, a, ret_addr] (b must be 0)
13 "RIGHT", "RIGHT", "DEC", "LEFT", "OR", "BUBBLE", # [temp, flag_reject, ret_addr] at temp
14 *load_number(len(accept) + 1), "BNZ", # skip if nonzero
15 *accept, # accept flag
16 *load_number(len(reject) + 1), "BZ", # skip if nonzero
17 *reject, # reject flag
18 "RIGHT",
19 *call_function("thank_user"),
20 "RIGHT", "JUMP" # return from main
21])
The CTF
This was the intended flag for the program: corctf{aHAhaHHAaAaAAAAhAhhahAaAAAaAAhhaHahA}
This challenge was released 24 hours into corCTF, and was solved by two teams, making it the hardest rev challenge in the CTF. Although I’m pretty satisfied with the results, I feel like the challenge could’ve been made improved by making more control flow decisions dependent on the flag’s data. The current program operated “blindly” on the flag data, so a simulator could easily trace the symbolic relationship between the flag payload and the program result without the state space blowing up. Next time, I’ll be sure to put a more complex algorithm inside my VM.
I actually made some mistakes in my flag verifier program, and teams discovered another flag that also got accepted. Oops! Next time, I will make sure to have more quality assurance and code reviews on my challenges.
Additionally, since I put so much effort into making a sophisticated assembler, I probably could’ve written another layer of virtualization within the VM to force players to carefully decipher how the entire VM worked, rather than just fuzzing and diffing pieces to get a rough estimate of what was going on.
The Conclusion
bubble-vm doesn’t have explicit push, pop, read, write, call, or return instructions,
and barely even supports random indexing,
yet through careful manipulation of memory layouts and tape positions, we can create powerful abstractions which
allow us to scale programs far beyond what a human can statically analyze. Even with extremely limiting architectures,
complex behaviors can emerge from a handful of primtive constructions, allowing us to model any computable problem.
I had a lot of fun creating this VM and writing my own program and assembler for it. Working on this challenge has definitely changed my viewpoint on computing and program design, and I hope to continue to write more cool projects and CTF challenges in the future.